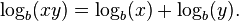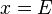Hecho Por
Kimberly Reyes
Ana Ovalles
Faider Bastidas
Se Agradece Su Atención Y Uso A Nuestra App Es Bastante Sencilla Pero Muy Entretenida Para Niños Que Quieren Aprender De Una Forma Divertida Las Matemáticas Y Por Que No Con Un Juego Para Niños Que Los Ayude A Reconocer Las Operaciones Básicas De La Matemática
domingo, 15 de mayo de 2016
App Inventor En Tu Celular
Para Poder Utilizar Las Apps Que Hiciste Debes Descargar La App Mitt Inventor En Tu Telefono Y Te Pedira Un Codigo Como Este


Requisitos Del Equipo
Requisitos del sistema:
PC y sistema operativo
Macintosh (con procesador Intel): Mac OS X 10.5, 10.6
Windows: Windows XP, Windows Vista, Windows 7
GNU / Linux: Ubuntu 8 +, 5 + Debian
Navegador
Mozilla Firefox 3.6 o superior
Nota: Si estás utilizando Firefox con el complemento NoScript, deberás desactivarlo, ya que App Inventor utiliza Javascript. Mira la nota en la página de solución de problemas .
Apple Safari 5.0 o superior
Google Chrome 4.0 o superior
Microsoft Internet Explorer 7 o superior
Pon a prueba tu configuración de Java
Tu ordenador debe ejecutar Java 6 (también conocido como Java 1.6) o superior. Puedes descargar Java desde www.java.com .
Pon a prueba tu configuración de Java mediante la realización de las dos pruebas siguientes:
Visite la página de prueba de Java . Usted debe ver un mensaje que Java está funcionando y que es la versión Java 1.6 o posterior.
Ejecute la prueba de AppInventor de Java haciendo clic en este enlace . Esto comprueba que tu navegador está configurado correctamente para ejecutar Java, y que tu equipo puede ejecutar aplicaciones con Java Web Start.
App Inventor no va a funcionar en tu ordenador si estas pruebas no tienen éxito. No intentes usar App Inventor hasta que no hayas resuelto este problema..
Ejecuta el software de instalación de App Inventor
Antes de poder utilizar App Inventor es necesario instalar algún software en tu ordenador. El software necesario se proporciona en un paquete llamado Configuración de App Inventor . Sigue las instrucciones para tu sistema operativo con el fin de hacer la instalación, y luego pasar a construir la aplicación de demostración (Hello Purr) con el teléfono o con el emulador.
PC y sistema operativo
Macintosh (con procesador Intel): Mac OS X 10.5, 10.6
Windows: Windows XP, Windows Vista, Windows 7
GNU / Linux: Ubuntu 8 +, 5 + Debian
Navegador
Mozilla Firefox 3.6 o superior
Nota: Si estás utilizando Firefox con el complemento NoScript, deberás desactivarlo, ya que App Inventor utiliza Javascript. Mira la nota en la página de solución de problemas .
Apple Safari 5.0 o superior
Google Chrome 4.0 o superior
Microsoft Internet Explorer 7 o superior
Pon a prueba tu configuración de Java
Tu ordenador debe ejecutar Java 6 (también conocido como Java 1.6) o superior. Puedes descargar Java desde www.java.com .
Pon a prueba tu configuración de Java mediante la realización de las dos pruebas siguientes:
Visite la página de prueba de Java . Usted debe ver un mensaje que Java está funcionando y que es la versión Java 1.6 o posterior.
Ejecute la prueba de AppInventor de Java haciendo clic en este enlace . Esto comprueba que tu navegador está configurado correctamente para ejecutar Java, y que tu equipo puede ejecutar aplicaciones con Java Web Start.
App Inventor no va a funcionar en tu ordenador si estas pruebas no tienen éxito. No intentes usar App Inventor hasta que no hayas resuelto este problema..
Ejecuta el software de instalación de App Inventor
Antes de poder utilizar App Inventor es necesario instalar algún software en tu ordenador. El software necesario se proporciona en un paquete llamado Configuración de App Inventor . Sigue las instrucciones para tu sistema operativo con el fin de hacer la instalación, y luego pasar a construir la aplicación de demostración (Hello Purr) con el teléfono o con el emulador.
Telefonos Compatibles
Hay cientos de diferentes modelos de teléfonos Android, y continuamente aparecen nuevos modelos. Incluso podemos no tener noticia sobre alguno de ellos. Éstos son algunos de los teléfonos que se están utilizando con éxito con App Inventor:
Google: Nexus One, Nexus S
Motorola: Droid, Droid X, Droid Incredible
T-Mobile: G1
HTC: Incredible, Hero, Desire
LG: Optimus Me
Tenga en cuenta, sin embargo, que en alguno de estos teléfonos será necesario instalar el controlador adecuado para trabajar con Windows.
Sea cual sea tu modelo, el teléfono debe tener instalada una tarjeta SD, o de lo contrario no funcionará con App Inventor.
Incluso si tu teléfono Android no está en esta lista, es probable que siga trabajando con App Inventor, pero no lo podemos decir con seguridad. Sigue las instrucciones que aparecen en esta página y, en caso que se presenten dificultades, consulta la página de solución de problemas , o busca ayuda en el Foro de Usuarios en la sección "Cómo instalar y conectar el teléfono" para recibir el consejo de otras personas que puedan estar usando el mismo teléfono.
Google: Nexus One, Nexus S
Motorola: Droid, Droid X, Droid Incredible
T-Mobile: G1
HTC: Incredible, Hero, Desire
LG: Optimus Me
Tenga en cuenta, sin embargo, que en alguno de estos teléfonos será necesario instalar el controlador adecuado para trabajar con Windows.
Sea cual sea tu modelo, el teléfono debe tener instalada una tarjeta SD, o de lo contrario no funcionará con App Inventor.
Incluso si tu teléfono Android no está en esta lista, es probable que siga trabajando con App Inventor, pero no lo podemos decir con seguridad. Sigue las instrucciones que aparecen en esta página y, en caso que se presenten dificultades, consulta la página de solución de problemas , o busca ayuda en el Foro de Usuarios en la sección "Cómo instalar y conectar el teléfono" para recibir el consejo de otras personas que puedan estar usando el mismo teléfono.
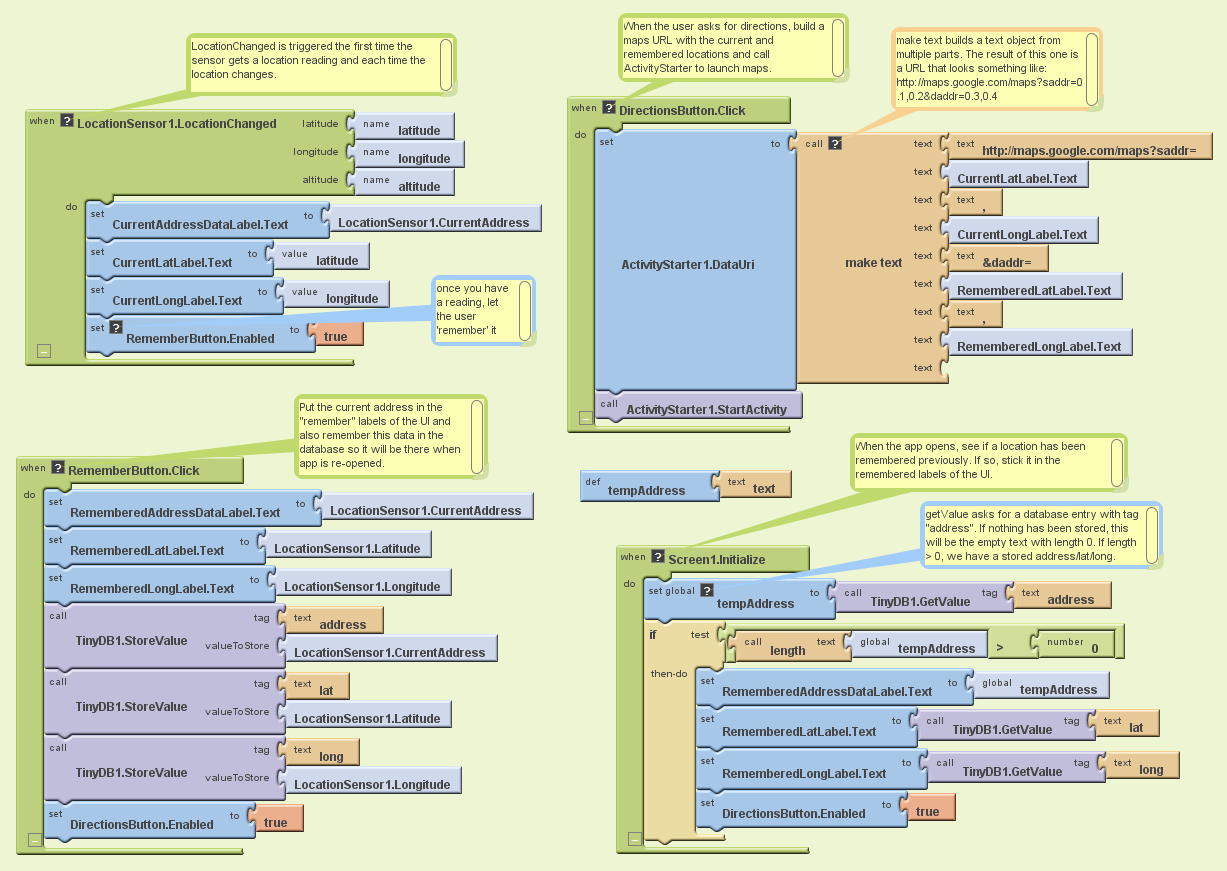
Como Hacer El Juego De Sonido
Con el Editor de bloques vamos a definir la forma en que la aplicación se va a comportar. Le diremos a los componentes lo que deben hacer y cuándo hacerlo. Vas a decirle al botón, que reproduzca el sonido del maullido cuando el usuario lo toque. Si los componentes son los ingredientes de una receta, puedes pensar en bloques como las instrucciones de elaboración del plato.
El editor de bloques tiene dos pestañas en la esquina superior izquierda: Integrados (Built-in) y mis bloques (My blocks) . Los botones situados debajo de cada pestaña muestran los bloques cuando se hace clic. Los Integrados son un conjunto de bloques genérico, que encontraremos disponibles independientemente de la aplicación que vayamos a crear. Son siempre los mismos. Los bloques debajo de la pestaña de mis bloques contienen bloques específicos, vinculados con el conjunto de componentes que hemos elegido para la aplicación. Varían según los componentes seleccionados previamente y cambian si cambiamos componentes sobre la marcha.
El editor de bloques tiene dos pestañas en la esquina superior izquierda: Integrados (Built-in) y mis bloques (My blocks) . Los botones situados debajo de cada pestaña muestran los bloques cuando se hace clic. Los Integrados son un conjunto de bloques genérico, que encontraremos disponibles independientemente de la aplicación que vayamos a crear. Son siempre los mismos. Los bloques debajo de la pestaña de mis bloques contienen bloques específicos, vinculados con el conjunto de componentes que hemos elegido para la aplicación. Varían según los componentes seleccionados previamente y cambian si cambiamos componentes sobre la marcha.
Editor De Bloques
El diseñador (Designer) es una de las tres herramientas clave que utilizarás en la creación de aplicaciones. El segundo es el Editor de bloques. El tercero es el teléfono. Vamos a usar el Editor de bloques para asignar los comportamientos de los componentes, como qué debe suceder cuando el usuario de la aplicación presiona un botón.
El editor de bloques se ejecuta en una ventana separada. Al hacer clic en Abrir el editor de bloques (Open the Blocks Editor) de la ventana de diseño, el archivo de programa del editor de bloques se debe descargar y ejecutar. Este proceso puede tardar 30 segundos o más. Si no se abre el Editor de bloques, podría ser porque el navegador no está configurado para ejecutar aplicaciones Java descargadas de forma automática. Una vez descargado, veremos el archivo del editor de bloques, llamado AppInventorForAndroidCodeblocks.jnlp y debemos abrirlo. Una vez hecho esto, se activa Java, que nos solicitará si queremos ejecutar la aplicación, a lo que responderemos que sí. Entonces, la ventana del editor de bloques debe verse como se muestra abajo, con "cajones" para los bloques de programa a la izquierda, y un gran espacio vacío para la colocación de los bloques que uniremos para montar el programa, que se va a hacer a continuación.
El editor de bloques se ejecuta en una ventana separada. Al hacer clic en Abrir el editor de bloques (Open the Blocks Editor) de la ventana de diseño, el archivo de programa del editor de bloques se debe descargar y ejecutar. Este proceso puede tardar 30 segundos o más. Si no se abre el Editor de bloques, podría ser porque el navegador no está configurado para ejecutar aplicaciones Java descargadas de forma automática. Una vez descargado, veremos el archivo del editor de bloques, llamado AppInventorForAndroidCodeblocks.jnlp y debemos abrirlo. Una vez hecho esto, se activa Java, que nos solicitará si queremos ejecutar la aplicación, a lo que responderemos que sí. Entonces, la ventana del editor de bloques debe verse como se muestra abajo, con "cajones" para los bloques de programa a la izquierda, y un gran espacio vacío para la colocación de los bloques que uniremos para montar el programa, que se va a hacer a continuación.
Importancia De App Inventor
En el actual diseño del Bachilleratose propone “Tecnologías de la Información y la Comunicación como asignatura optativa”. Entre los objetivos generales de esta asignatura se puede leer “Usar los recursos informáticos como instrumento de resolución de problemas específicos” o “Integrar la información textual, numérica y gráfica obtenida de cualquier fuente para elaborar contenidos propios y publicarlos ... y formatos que faciliten la inclusión de elementos multimedia decidiendo la forma en la que se ponen a disposición del resto de usuarios”. Son muchos los profesores que enseñan algún lenguaje de programación como una de las herramientas para alcanzar estos objetivos.
En este artículo se propone usar App Inventor1 como parte del curriculum de esta asignatura. App Inventor es al mismo tiempo un lenguaje de programación, una herramienta de diseño y un entorno de desarrollo de aplicaciones para móviles y tablets que funcionen con el sistema operativo Android. App Inventor permite también ejecutar las aplicaciones en un emulador, por lo que no es imprescindible disponer del teléfono para probar los programas que se hagan.
En este artículo se propone usar App Inventor1 como parte del curriculum de esta asignatura. App Inventor es al mismo tiempo un lenguaje de programación, una herramienta de diseño y un entorno de desarrollo de aplicaciones para móviles y tablets que funcionen con el sistema operativo Android. App Inventor permite también ejecutar las aplicaciones en un emulador, por lo que no es imprescindible disponer del teléfono para probar los programas que se hagan.
Instalación De App Inventor
Puedes configurar la aplicación Inventor y empezar a crear aplicaciones en cuestión de minutos. El Diseñador y Editor de bloques se ejecutan ahora por completo en el navegador (la nube!). Para ver tu aplicación en un dispositivo mientras lo construyes (también llamada "Probando en vivo"), tendrás que seguir los pasos que se muestran a continuación.
Tienes tres opciones para configurar las pruebas en vivo, mientras construyes aplicaciones.
1.- Si estás utilizando un dispositivo Android y tienes una conexión inalámbrica a Internet (WiFi), puedes comenzar la creación de aplicaciones sin necesidad de descargar ningún software en su ordenador. Eso sí, tendrás que instalar la aplicación Companion App Inventor en tu dispositivo. Elige la opción uno. Esta opción se recomienda encarecidamente.
2.- Si no tienes un dispositivo Android, tendrás que instalar el software en su ordenador para que pueda utilizar el emulador de Android en la pantalla del mismo. Elige la opción dos.
3.- Si no tienes una conexión inalámbrica a Internet (WiFi), tendrás que instalar el software en tu computadora de modo que puedas conectar a su dispositivo Android a través de USB. Elige la opción de tres. La opción de conexión USB puede ser complicada, especialmente en Windows. Usa esto como un último recurso.
Tienes tres opciones para configurar las pruebas en vivo, mientras construyes aplicaciones.
1.- Si estás utilizando un dispositivo Android y tienes una conexión inalámbrica a Internet (WiFi), puedes comenzar la creación de aplicaciones sin necesidad de descargar ningún software en su ordenador. Eso sí, tendrás que instalar la aplicación Companion App Inventor en tu dispositivo. Elige la opción uno. Esta opción se recomienda encarecidamente.
2.- Si no tienes un dispositivo Android, tendrás que instalar el software en su ordenador para que pueda utilizar el emulador de Android en la pantalla del mismo. Elige la opción dos.
3.- Si no tienes una conexión inalámbrica a Internet (WiFi), tendrás que instalar el software en tu computadora de modo que puedas conectar a su dispositivo Android a través de USB. Elige la opción de tres. La opción de conexión USB puede ser complicada, especialmente en Windows. Usa esto como un último recurso.
En Que Consiste El Juego
El Juego Mathemath Es Muy Básico, Es Un Juego Parecido A Presiona El Topo Pero Con Las Cuatro Operaciones Básicas De La Matemática ( Suma, Resta, Multiplicación y División ) El Cual Consiste En Presionar Las Cuatro Operaciones Antes De Que Aparezcan En Otro Lugar De La Ventana. Hay Un Contador De Aciertos Como De Desaciertos Y Hay Un Botón Que Restaura Todos Los Marcadores. Los Iconos De Las Operaciones Desaparecen Cada Segundo Y Cada Vez Que Se Presiona Una De Estas Operaciones Vibra El Celular Teniendo Una Excelente Respuesta De Este Juego .
Por Que Usar App Inventor
App Inventor Es Una Aplicación De Google Bastante Fácil De Utilizar Que Permite A Estudiantes O Gente No Profesional En EL Tema Tecnológico Les Permite Desarrollar Aplicaciones Sin Ninguna Complicación Tanto De Juegos Como De Información.
Caracteristicas De App Inventor
El editor de bloques de la plataforma App Inventor, utiliza la librería Open Blocks de Java para crear un lenguaje visual a partir de bloques. Estas librerías están distribuidas por Massachusetts Institute of Technology (MIT) bajo su licencia libre (MIT License). El compilador que traduce el lenguaje visual de los bloques para la aplicación en Android utiliza Kawa como lenguaje de programación, distribuido como parte del sistema operativo GNU de la Free Software Foundation
App Inventor pueden tener su primera aplicación en funcionamiento en una hora o menos, y se pueden programar aplicaciones más complejas en mucho menos tiempo que con los lenguajes más tradicionales, basados en texto. Inicialmente desarrollado por el profesor Hal Abelson y un equipo de Google Educación, mientras que Hal pasaba un año sabático en Google, App Inventor se ejecuta como un servicio Web administrado por personal del Centro del MIT para el aprendizaje móvil –una colaboración de MIT de Ciencia Computacional e Inteligencia Artificial de laboratorio (CSAIL) y el Laboratorio de Medios del MIT–. Inventor MIT App es compatible con una comunidad mundial de casi dos millones de usuarios que representan a 195 países en todo el mundo. Más de 85 mil usuarios semanales activas de la herramienta han construido más de 4,7 millones de aplicaciones de Android. Una herramienta de código abierto que pretende realizar la programación y la creación de aplicaciones accesibles a una amplia gama de audiencias.
App Inventor pueden tener su primera aplicación en funcionamiento en una hora o menos, y se pueden programar aplicaciones más complejas en mucho menos tiempo que con los lenguajes más tradicionales, basados en texto. Inicialmente desarrollado por el profesor Hal Abelson y un equipo de Google Educación, mientras que Hal pasaba un año sabático en Google, App Inventor se ejecuta como un servicio Web administrado por personal del Centro del MIT para el aprendizaje móvil –una colaboración de MIT de Ciencia Computacional e Inteligencia Artificial de laboratorio (CSAIL) y el Laboratorio de Medios del MIT–. Inventor MIT App es compatible con una comunidad mundial de casi dos millones de usuarios que representan a 195 países en todo el mundo. Más de 85 mil usuarios semanales activas de la herramienta han construido más de 4,7 millones de aplicaciones de Android. Una herramienta de código abierto que pretende realizar la programación y la creación de aplicaciones accesibles a una amplia gama de audiencias.
Acerca De App Inventor
App Inventor es un entorno de desarrollo de aplicaciones para dispositivos Android. Para desarrollar aplicaciones con App Inventor sólo necesitas un navegador web y un teléfono o tablet Android (si no lo tienes podrás probar tus aplicaciones en un emulador). App Inventor se basa en un servicio web que te permitirá almacenar tu trabajo y te ayudará a realizar un seguimiento de sus proyectos.
Se trata de una herramienta de desarrollo visual muy fácil de usar, con la que incluso los no programadores podrán desarrollar sus aplicaciones.
Al construir las aplicaciones para Android trabajarás con dos herramientas: App Inventor Designer y App Inventor Blocks Editor. En Designer construirás el Interfaz de Usuario, eligiendo y situando los elementos con los que interactuará el usuario y los componentes que utilizará la aplicación. En el Blocks Editor definirás el comportamiento de los componentes de tu aplicación.
Se trata de una herramienta de desarrollo visual muy fácil de usar, con la que incluso los no programadores podrán desarrollar sus aplicaciones.
Al construir las aplicaciones para Android trabajarás con dos herramientas: App Inventor Designer y App Inventor Blocks Editor. En Designer construirás el Interfaz de Usuario, eligiendo y situando los elementos con los que interactuará el usuario y los componentes que utilizará la aplicación. En el Blocks Editor definirás el comportamiento de los componentes de tu aplicación.
Realizacion de la app
Se Realizo Una Aplicación En Una Herramienta De Internet Muy Buena Llamada App Inventor, La Cual Nos Permitió Crear Una App De Juego Básica, Donde Se Presionan En Tu Celular Las Operaciones Básicas Teniendo Aciertos Como Desaciertos Cuando Se Presiona Uno De Estas Operaciones Básicas Que Aparecen Allí Tu Celular Vibrara, Es Bastante Básica Pero Bastante Entretenida Debido A El Tiempo De Juego De Estas Mismas, Es Similar A Un Juego De Presiona Topo Pero Con Las Operaciones Matemáticas Básicas.
sábado, 14 de mayo de 2016
SUMA DE FRACCIONES
Sumar fracciones es un procedimiento bastante sencillo. Sin embargo, suelen aparecer inquietudes cuando ambas fracciones tienen denominadores diferentes. Aprende cómo resolver la suma de fracciones heterogéneas en esta corta infografía.
Fracción impropia
Una fracción impropia es aquella en la cual el numerador es mayor que el denominador. En este ejemplo, el cinco, que está en el lugar del numerador, es mayor que el cuatro, que ocupa el lugar del denominador.
Este tipo de fracciones pueden ser convertidas en un número mixto. Para averiguar cómo se hace, dirígete a nuestra lección de fracciones impropias.
Reducir y simplificar
Puede que al hacer la suma de fracciones heterogéneas te encuentres con que el resultado son fracciones bastante grandes como 20/12, 84/32, 106/80 o incluso fracciones más grandes.
Recuerda que este tipo de fracciones deben ser reducidas o simplificadas para hallar su equivalente. Averigua cómo hacerlo en nuestra lección de reducir fracciones.
LOGARITMO
el logaritmo de un número real positivo en una base de logaritmo determinadaes el exponente al cual hay que elevar la base para obtener dicho número. Por ejemplo, el logaritmo de 1000 en base 10 es 3, porque 1000 es igual a 10 a la potencia 3: 1000 = 103 = 10×10×10.
De la misma manera que la operación opuesta de la suma es la resta y la de la multiplicación la división, el cálculo de logaritmos es la operación inversa a la exponenciación de la base del logaritmo.
Para representar la operación de logaritmo en una determinada base se escribe la abreviatura log y como subíndice la base y después el número resultante del que deseamos hallar el logaritmo. Por ejemplo, 35=243 luego log3243=5. Cuando se sobreentiende la base, se puede omitir.
Los logaritmos fueron introducidos por John Napier a principios del siglo XVII como un medio de simplificación de los cálculos. Estos fueron prontamente adoptados por científicos, ingenieros, banqueros y otros para realizar operaciones fácil y rápidamente, usando reglas de cálculo y tablas de logaritmos. Estos dispositivos se basan en el hecho más importante poridentidades logarítmicas que el logaritmo de un producto es la suma de los logaritmos de los factores:
POLÍGONO
En geometría, un polígono es una figura plana compuesta por una secuencia limitada de segmentos rectos consecutivos que cierran una región en el plano. Estos segmentos son llamados lados, y los puntos en que se intersectan se llaman vértices. El interior del polígono es llamado área. El polígono es el caso bidimensional del politopo, figura geométrica general definida para cualquier número de dimensiones. A su vez, un politopo de tres dimensiones se denomina poliedro, y de cuatro dimensiones se denomina polícoro.
Líneapoligonal Se denomina línea poligonal al conjunto de segmentos unidos sucesivamente por sus extremos (el extremo de cada segmento es origen del siguiente), tal que dos segmentos sucesivos no están alineados (en tal caso se considera como un único segmento). Las líneas poligonales pueden ser abiertas o cerradas, un polígono está conformado por una línea poligonal cerrada.
CALCULO
Las dos acepciones del cálculo (la general y la restringida) arriba definidas están íntimamente ligadas. El cálculo es una actividad natural y primordial en el hombre, que comienza en el mismo momento en que empieza a relacionar unas cosas con otras en un pensamiento o discurso. El cálculo lógico natural como razonamiento es el primer cálculo elemental del ser humano. El cálculo en sentido lógico-matemático aparece cuando se toma conciencia de esta capacidad de razonar y trata de formalizarse.
Por lo tanto, podemos distinguir dos tipos de operaciones:
- Operaciones orientadas hacia la consecución de un fin, como prever, programar, conjeturar, estimar, precaver, prevenir, proyectar, configurar, etc. que incluyen en cada caso una serie de complejas actividades y habilidades tanto de pensamiento como de conducta. En su conjunto dichas actividades adquieren la forma de argumento o razones que justifican una finalidad práctica o cognoscitiva.
- Operaciones formales como algoritmo que se aplica bien directamente a los datos conocidos o a los esquemas simbólicos de la interpretación lógico-matemática de dichos datos; las posibles conclusiones, inferencias o deducciones de dicho algoritmo son el resultado de la aplicación de reglas estrictamente establecidas de antemano.
- Resultado que es:
- Conclusión de un proceso de razonamiento.
- Resultado aplicable directamente a los datos iniciales (resolución de problemas).
- Modelo de relaciones previamente establecido como teoría científica y significativo respecto a determinadas realidades (Creación de modelos científicos).
- Mero juego formal simbólico de fundamentación, creación y aplicación de las reglas que constituyen el sistema formal del algoritmo (Cálculo lógico-matemático, propiamente dicho).
Dada la importancia que históricamente ha adquirido la actividad lógico-matemática en la cultura humana el presente artículo se refiere a este último sentido. De hecho la palabra, en su uso habitual, casi queda restringida a este ámbito de aplicación; para algunos, incluso, queda reducida a un solo tipo de cálculo matemático, pues en algunas universidades se llamaba "Cálculo" a una asignatura específica de cálculo matemático (como puede ser el cálculo infinitesimal, análisis matemático, cálculo diferencial e integral, etc.).
En un artículo general sobre el tema no puede desarrollarse el contenido de lo que supone el cálculo lógico-matemático en la actualidad. Aquí se expone solamente el fundamento de sus elementos más simples, teniendo en cuenta que sobre estas estructuras simples se construyen los cálculos más complejos tanto en el aspecto lógico como en el matemático.
ARITMÉTICA
La aritmética es la rama de la matemática cuyo objeto de estudio son los números y las operaciones elementales hechas con ellos: adición, resta, multiplicación y división.
Al igual que en otras áreas de la matemática, como el álgebra o la geometría, el sentido de «la aritmética» ha ido evolucionando con el progresivo desarrollo de las ciencias. Originalmente, la aritmética se desarrolla de manera formal en la Antigua Grecia, con el refinamiento del rigor matemático y las demostraciones, y su extensión a las distintas disciplinas de las «ciencias naturales». En la actualidad, puede referirse a la aritmética elemental, enfocada a la enseñanza de la matemática básica; también al conjunto que reúne el cálculo aritmético y las operaciones matemáticas, específicamente, las cuatro operaciones básicas aplicadas ya sea a números (naturales, fracciones, etc.) como a entidades matemáticas más abstractas (matrices, operadores, etc); también a la así llamada alta aritmética,3 mejor conocida como teoría de números.
ECUACIÓN LINEAL
Una ecuación de primer grado o ecuación lineal significa que es un planteamiento de igualdad, involucrando una o más variables a la primera potencia, que no contiene productos entre las variables, es decir, una ecuación que involucra solamente sumas y restas de una variable a la primera potencia. En todo anillo conmutativo pueden definirse ecuaciones de primer grado.EN UNA INCÓGNITA
Una ecuación de una variable 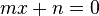 definida sobre un cuerpo
definida sobre un cuerpo  , es decir, con
, es decir, con 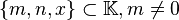 donde x es la variable, admite la siguiente solución:
donde x es la variable, admite la siguiente solución:
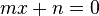 definida sobre un cuerpo
definida sobre un cuerpo  , es decir, con
, es decir, con 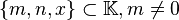 donde x es la variable, admite la siguiente solución:
donde x es la variable, admite la siguiente solución:
En dos incógnitas En el sistema cartesiano representan rectas. Una forma común de las ecuaciones lineales de dos variables es: 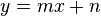 ; Donde
; Donde  representa la pendiente y el valor de
representa la pendiente y el valor de  determina el punto donde la recta corta al eje Y (la ordenada al origen). Algunos ejemplos de ecuaciones lineales:
determina el punto donde la recta corta al eje Y (la ordenada al origen). Algunos ejemplos de ecuaciones lineales: 
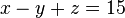

- Formas alternativas
Formas complejas como las anteriores pueden reescribirse usando las reglas del álgebra elemental en formas más simples. Las letras mayúsculas representan constantes, mientras x e y son variables.
Ecuación general
-
- Aquí A y B no son ambos cero. Representa una línea en el cartesiano. Es posible encontrar los valores donde x e y se anulan.
- Ecuación segmentaria o simétrica
-
- Aquí ni E ni F no pueden ser cero. El gráfico de esta ecuación corta al eje X y al eje Y en E y F respectivamente.
- Forma paramétrica
- Dos ecuaciones que deben cumplirse de manera simultanea, cada una en la variable t. Puede convertirse a la forma general despejando t en ambas ecuaciones e igualando. En esta representación puede afirmarse que la recta pasa por el punto
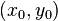 y forma con el eje de abcisas un ángulo cuya tangente satisface:
y forma con el eje de abcisas un ángulo cuya tangente satisface: 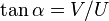
- Casos especiales:
-
- Un caso especial es la forma estándar donde
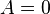 y
y 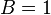 . El gráfico es una línea horizontal sin intersección con el eje X o (si F = 0) coincidente con ese eje.
. El gráfico es una línea horizontal sin intersección con el eje X o (si F = 0) coincidente con ese eje.
- Otro caso especial de la forma general donde
 y
y  . El gráfico es una línea vertical, interceptando el eje X en E.
. El gráfico es una línea vertical, interceptando el eje X en E.
- En este caso, todas las variables fueron canceladas, dejando una ecuación que es verdadera en todos los casos. La forma original (no una tan trivial como la del ejemplo), es llamada identidad. El gráfico es todo el plano cartesiano, ya que lo satisface todo par de números reales x e y.
Nótese que si la manipulación algebraica lleva a una ecuación como 1 = 0 entonces la original es llamada inconsistente, o sea que no se cumple para ningún par de números x ey. Un ejemplo podría ser:  .
.
 .
.
Adicionalmente podría haber más de dos variables, en ecuaciones simultáneas. Para más información véa: Sistema lineal de ecuaciones.
Ecuación lineal en el espacio n-dimensional Las ecuaciones lineales de varias variables admiten también interpretaciones geométricas,cuando los coeficientes de la ecuación pertenecen a un cuerpo. Así una función lineal de dos variables de la forma 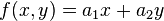 representa una recta en un plano. En varias variables asumiendo que tanto las variables
representa una recta en un plano. En varias variables asumiendo que tanto las variables  y los coeficientes
y los coeficientes  , donde
, donde  es un cuerpo entonces una ecuación lineal como la siguiente:
es un cuerpo entonces una ecuación lineal como la siguiente:  representa un hiperplano de n-1 dimensiones en el espacio vectorial n-dimensional Sistemas de ecuaciones lineales Los sistemas de ecuaciones lineales expresan varias ecuaciones lineales simultáneamente y admiten un tratamiento matricial. Para su resolución debe haber tantas ecuaciones como incógnitas y el determinante de la matriz ha de ser real y no nulo. Geométricamente corresponden a intersecciones de líneas en un único punto (sistema lineal de dos ecuaciones con dos incógnitas), planos en una recta (dos ecuaciones lineales de tres incógnitas) o un único punto (tres ecuaciones lineales de tres incógnitas). Los casos en los que el determinante de la matriz es nulo no poseen solución.
representa un hiperplano de n-1 dimensiones en el espacio vectorial n-dimensional Sistemas de ecuaciones lineales Los sistemas de ecuaciones lineales expresan varias ecuaciones lineales simultáneamente y admiten un tratamiento matricial. Para su resolución debe haber tantas ecuaciones como incógnitas y el determinante de la matriz ha de ser real y no nulo. Geométricamente corresponden a intersecciones de líneas en un único punto (sistema lineal de dos ecuaciones con dos incógnitas), planos en una recta (dos ecuaciones lineales de tres incógnitas) o un único punto (tres ecuaciones lineales de tres incógnitas). Los casos en los que el determinante de la matriz es nulo no poseen solución. Si se consideran n ecuaciones de primer grado linealmente independientes definidas sobre un cuerpo entonces existe solución única para el sistema si se dan las condiciones del teorema de Rouché-Frobenius, que puede ser calculada mediante la regla de Cramer que es aplicable a cualquier cuerpo. Si las ecuaciones no son linealmente independientes o no se dan las condiciones del teorema la situación es más complicada. Si el sistema se plantea sobre un anillo conmutativo que no sea un cuerpo, la existencia de soluciones es también más complejas. LINEALIDAD Una función definida sobre un espacio vectorial es lineal si y solo si se cumple con la siguiente proposición:
Si se consideran n ecuaciones de primer grado linealmente independientes definidas sobre un cuerpo entonces existe solución única para el sistema si se dan las condiciones del teorema de Rouché-Frobenius, que puede ser calculada mediante la regla de Cramer que es aplicable a cualquier cuerpo. Si las ecuaciones no son linealmente independientes o no se dan las condiciones del teorema la situación es más complicada. Si el sistema se plantea sobre un anillo conmutativo que no sea un cuerpo, la existencia de soluciones es también más complejas. LINEALIDAD Una función definida sobre un espacio vectorial es lineal si y solo si se cumple con la siguiente proposición:
 donde α es cualquier escalar. También se llama a f operador lineal
donde α es cualquier escalar. También se llama a f operador lineal
FUNCIONES
En matemáticas, se dice que una magnitud o cantidad es funcion de otra si es una relación entre dos magnitudes, de tal manera que a cada valor de la primera le corresponde un único valor de la segunda, llamada imagen. Por ejemplo el área A de un círculo es función de su radio r (el valor del área es proporcional al cuadrado del radio, A = π·r2). Del mismo modo, la duración T de un viaje en tren entre dos ciudades separadas por una distancia d de 150 km depende de la velocidad v a la que se desplace el tren (la duración es inversamente proporcional a la velocidad, d / v). A la primera magnitud (el área, la duración) se la denomina variable dependiente, y la cantidad de la que depende (el radio, la velocidad) es la variable independiente.
En análisis matemático, el concepto general de función, aplicación o mapeo se refiere a una regla que asigna a cada elemento de un primer conjunto un único elemento de un segundo conjunto (correspondencia matemática). Por ejemplo, cada número entero posee un único cuadrado, que resulta ser un número natural (incluyendo el cero):
| ... | −2 → +4, | −1 → +1, | 0 → 0, | |
| +1 → +1, | +2 → +4, | +3 → +9, | ... |
Esta asignación constituye una función entre el conjunto de los números enteros Z y el conjunto de los números naturales N. Aunque las funciones que manipulan números son las más conocidas, no son el único ejemplo: puede imaginarse una función que a cada palabra del español le asigne su letra inicial:
| ..., | Estación → E, | Museo → M, | Arroyo → A, | Rosa → R, | Avión → A, | ... |
Esta es una función entre el conjunto de las palabras del español y el conjunto de las letras del alfabeto español.
La manera habitual de denotar una función f es:
- f: A → B
- a → f(a),
donde A es el dominio de la función f, su primer conjunto o conjunto de partida; y B es el codominio de f, su segundo conjunto o conjunto de llegada. Por f(a) se denota la regla o algoritmo para obtener la imagen de un cierto objeto arbitrario a del dominio A, es decir, el (único) objeto de B que le corresponde. En ocasiones esta expresión es suficiente para especificar la función por completo, infiriendo el dominio y codominio por el contexto. En el ejemplo anterior, las funciones «cuadrado» e «inicial», llámeseles f y g, se denotarían entonces como:
- f: Z → N
- k → k2, o sencillamente f(k) = k2;
- g: V → A
- p → Inicial de p;
si se conviene V = {Palabras del español} y A = {Alfabeto español}.
Una función puede representarse de diversas formas: mediante el citado algoritmo o ecuaciones para obtener la imagen de cada elemento, mediante una tabla de valores que empareje cada valor de la variable independiente con su imagen —como las mostradas arriba—, o como una gráfica que dé una imagen de la función.
Suscribirse a:
Comentarios (Atom)